Matemático encuentra triples pitagóricos en una tablilla babilónica antigua

 

Un matemático de la Universidad de Nueva Gales del Sur en Sydney ha descubierto el ejemplo más antiguo de geometría aplicada jamás registrado, informa la sala de redacción de la universidad . La tablilla ilustra el uso de triples pitagóricos para dividir la tierra, 1.100 años antes de que el matemático griego Pitágoras registrara el principio geométrico.

En un mapa de tablillas de arcilla babilónica de 3.700 años recuperado en Irak hace más de 100 años, el Dr. Daniel Mansfield ha identificado una forma avanzada de matemáticas que se utilizó para dividir una gran parcela de tierra en secciones geométricamente precisas. Sorprendentemente, esta geometría aplicada se basó en un principio matemático que no se descubriría oficialmente hasta que hubieran pasado otros 11 siglos.

El Dr. Mansfield, sosteniendo la tablilla de arcilla babilónica con evidencia del uso de Triples pitagóricos. ( UNSW Sydney )

Los triples pitagóricos, como resulta, ¡son una idea babilónica!

La tablilla de arcilla babilónica en cuestión, que se conoce como Si. 427 , se ha mantenido en exhibición en un museo en Estambul desde que fue descubierto por primera vez en el siglo XIX. Se ha relacionado con la época del Primer o Antiguo Imperio Babilónico , que primero estableció y luego gobernó el antiguo estado de Babilonia en Mesopotamia (lo que hoy es Irak y Siria ) desde el siglo XIX a.C. hasta el siglo XVI a.C.

Las inscripciones en el reverso revelaron que la tableta se había utilizado como una especie de mapa, específicamente de parcelas de tierra propiedad de varias personas. Pero la verdadera historia de su creación había permanecido oculta, hasta que apareció Daniel Mansfield y la miró con una nueva perspectiva.

El anverso (anverso) de la tablilla de arcilla babilónica Si.427. Las inscripciones en el reverso revelaron que la tableta se había utilizado como una especie de mapa, específicamente de parcelas de tierra propiedad de varias personas y esto ayudó al Dr. Daniel Mansfield a descubrir que los triples pitagóricos en realidad se inventaron mucho antes de que Pitágoras obtuviera el crédito por ellos. Fotografía y cortesía del İstanbul Arkeoloji Müzeleri. ( Fundamentos de la ciencia )

Como explica el Dr. Mansfield en un artículo publicado en la última edición de Foundations of Science , el cartógrafo / agrimensor babilónico estaba haciendo uso de un importante principio matemático, conocido como el triple pitagórico, para realizar su trabajo correctamente.

Un triple pitagórico consta de tres números enteros, los dos primeros al cuadrado serán iguales al tercero al cuadrado (es decir, 3² + 4² = 5², o 9 + 16 = 25). Este principio se puede utilizar para crear triángulos precisos en ángulo recto, con las líneas verticales y horizontales igualando los dos primeros números y la línea diagonal igualando el tercero. Es por eso que el concepto detrás de los triples pitagóricos (el famoso Teorema de Pitágoras) se clasifica como un principio de trigonometría (la geometría de los triángulos).

Entonces, si las líneas perpendiculares que se juntan para formar un ángulo recto se dibujan en longitudes de tres y cuatro unidades, la línea diagonal que conecta sus extremos para formar un triángulo tendrá exactamente cinco unidades de largo, cada vez. Es importante tener en cuenta que los triples pitagóricos se pueden usar para hacer tanto rectángulos exactos como triángulos exactos, ya que un rectángulo se puede dividir en dos triángulos rectángulos colocados uno encima del otro.

Esta no es solo una fórmula matemática abstracta. Ofrece una forma de crear formas exactas a partir de líneas perfectamente perpendiculares en situaciones del mundo real.

Entre sus muchos usos prácticos, los triples pitagóricos se pueden usar para dividir una sección de tierra en secciones triangulares o rectangulares más pequeñas de tamaños y formas iguales. Eso es lo que estaba tratando de hacer la persona que creó la tablilla de arcilla Si.427. Y con la ayuda de un principio matemático avanzado, pudo hacer un trabajo sobresaliente.

Este concepto matemático fue supuestamente descubierto por primera vez por Pitágoras , el legendario filósofo , matemático y místico griego que vivió en el siglo VI a. C. Como deja en claro la investigación del Dr. Mansfield, lo que realmente hizo Pitágoras fue redescubrir un principio que los babilonios ya entendían y usaban 1.100 años antes de que él naciera.

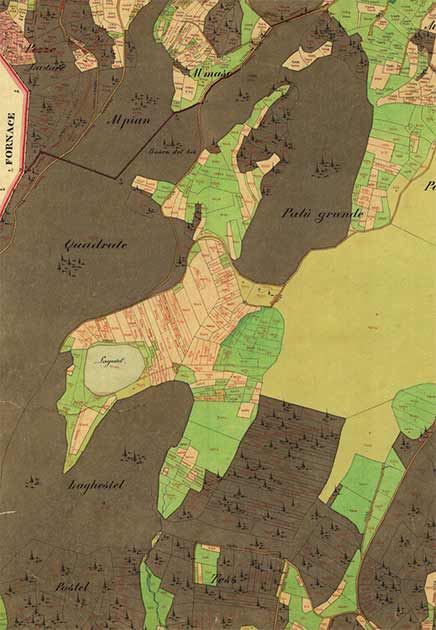
Un antiguo mapa catastral de 1780 de Laghestel di Piné, región de Trentino-Alto Adige en Italia (De Catasto Teresiano, Archivo del "Libro fondiario e Catasto", Trento). Basándose en la investigación del Dr. Mansfield, pudo demostrar que los mapas catastrales babilónicos se basaban en triples pitagóricos. ( Capítulo del libro Mapping Synusiae )

Resolución de problemas mediante trigonometría en el antiguo babilonio

El mapa de tierras en tablillas de arcilla S.427 no se creó con el propósito de mantener registros simples. “Si.427 se trata de un terreno que se está vendiendo”, explicó el Dr. Mansfield. “Es el único ejemplo conocido de un documento catastral del período OB [Antiguo Babilónico], que es un plan utilizado por los topógrafos para definir los límites de la tierra. En este caso, nos brinda detalles legales y geométricos sobre un campo que se divide después de que parte de él se vendió ".

Los detalles sobre el propósito de la tablilla se revelan en escritura cuneiforme antigua escrita en el reverso de la tablilla. Esto fue descifrado hace mucho tiempo, y resultó ser una descripción de la tierra agrícola que se estaba dividiendo y algunas de sus características.

Se han recuperado y descodificado muchos documentos de la era babilónica antigua, y en varios se hace mención de un importante terrateniente llamado Sin-bel-apli, que aparentemente poseía al menos algunas de las propiedades representadas en el rostro de Si.427.

Un mapa de tablillas de arcilla de Babilonia del mundo, 700-500 a. C. (Gary Todd / CC0 )

“Otra tableta se refiere a una disputa entre Sin-bel-apli, un individuo prominente mencionado en muchas tabletas, incluida la Si.427, y una rica terrateniente”, dijo la Dra. Mansfield. "La disputa es por valiosas palmeras datileras en la frontera entre sus dos propiedades".

“El administrador local acepta enviar un topógrafo para resolver la disputa”, continuó. "Al igual que lo haríamos hoy, hay individuos privados tratando de averiguar dónde están sus límites terrestres, y el topógrafo sale, pero en lugar de usar un equipo de GPS, usan triples pitagóricos".

¿Se creó Si.427 para ayudar a resolver un desacuerdo sobre quién era dueño de un bosque de palmeras datileras? ¿O se usó este documento para facilitar otra transacción de tierras que involucró al poderoso e influyente Sin-bel-apli?

Esta pregunta no se puede responder de manera definitiva. Pero lo que se puede decir con certeza es que los antiguos babilonios utilizaron las matemáticas para desarrollar soluciones racionales a problemas espinosos. Si bien la gente podía mentir, deben haber razonado, los números nunca lo harían.

“Nadie esperaba que los babilonios estuvieran usando triples pitagóricos de esta manera”, se maravilló el Dr. Mansfield. "Es más parecido a las matemáticas puras, inspirado en los problemas prácticos de la época".

La tablilla de arcilla babilónica Plimpton 322 alertó por primera vez al Dr. Mansfield sobre el hecho de que los mesopotámicos estaban interesados ​​en la trigonometría y que entendían las triples pitagóricas. Fotografía cortesía de la Biblioteca de libros raros y manuscritos de la Universidad de Columbia. (Andrew Kelly / Fundamentos de la ciencia )

Decodificando el genio matemático de los constructores babilónicos

Daniel Mansfield descubrió por primera vez el interés de los antiguos babilonios por la trigonometría a través de su estudio de otra tablilla de arcilla que se creó durante la época del Antiguo Imperio Babilónico.

Esta tablilla, conocida como Plimpton 322 , presentaba varias columnas de números que revelaban el interés de los babilonios por la trigonometría y su conocimiento del triple pitagórico. Sin embargo, desde que el coleccionista de artefactos George Plimpton donó esta tableta para su estudio en la década de 1930, los académicos habían luchado por explicar su verdadero significado y propósito.

Esto cambió en 2017, cuando el Dr. Mansfield y su colega de la UNSW Sydney Norman Wildberger publicaron un artículo en la revista Historia Mathematica explicando qué significaba realmente la tableta y cómo se había utilizado. La tabla trigonométrica intrincadamente preparada de Plimpton 322 no fue diseñada como un dispositivo de enseñanza, sino para su uso en proyectos del mundo real que requerían cálculos y mediciones precisas.

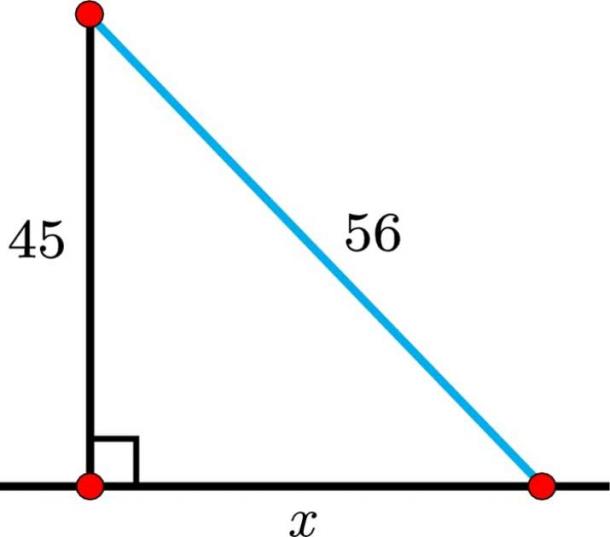
Basándose en la investigación del Dr. Mansfield, pudo demostrar que problemas como el anterior se estaban resolviendo en la época mesopotámica. Problema: suponga que una rampa que conduce a la parte superior de una pared en zigurat tiene 56 codos de largo y la altura vertical del zigurat es de 45 codos. ¿Cuál es la distancia x desde la base exterior de la rampa hasta el punto directamente debajo de la parte superior? ( Revista Historia Mathematica )

“Plimpton 322 era una herramienta poderosa que podría haber sido utilizada para topografía de campos o hacer cálculos arquitectónicos para construir palacios, templos o pirámides escalonadas”, dijo el Dr. Mansfield a un entrevistador de The Guardian en ese momento.

Las excavaciones en el área donde una vez reinó el Imperio Babilónico han descubierto muchos proyectos de construcción e infraestructura que demuestran los impresionantes logros de Babilonia en arquitectura e ingeniería. Esto incluye proyectos iniciados por los gobernantes del Antiguo Imperio Babilónico y por sus sucesores (el Imperio en su conjunto duró más de 1.200 años). Su logro más notable fue la creación de los Jardines Colgantes de Babilonia , una de las siete maravillas del mundo antiguo que los arqueólogos han estado tratando de localizar durante siglos.

En el nuevo artículo del Dr. Mansfield en Foundations of Science , explica cómo sus descubrimientos con respecto a Plimpton 322 lo llevaron en la dirección correcta mientras examinaba Si. 427. Una vez que se interpretó correctamente el primero, la verdad sobre el segundo se hizo muy clara.

“Una vez que se comprende qué son los triples pitagóricos, su sociedad ha alcanzado un nivel particular de sofisticación matemática”, dijo el Dr. Mansfield, expresando admiración por lo que los antiguos babilonios pudieron lograr.

No solo entendieron este importante principio 1.100 años antes de que Pitágoras supuestamente lo “inventara”, sino que supieron cómo aplicarlo en el mundo real. En la sociedad compleja que los constructores del antiguo imperio babilónico aspiraban a crear enfoques racionales para la resolución de problemas, habría sido esencial para su éxito.

Por Nathan Falde

https://www.ancient-origins.net/news-history-archaeology/pythagorean-triples-0015661